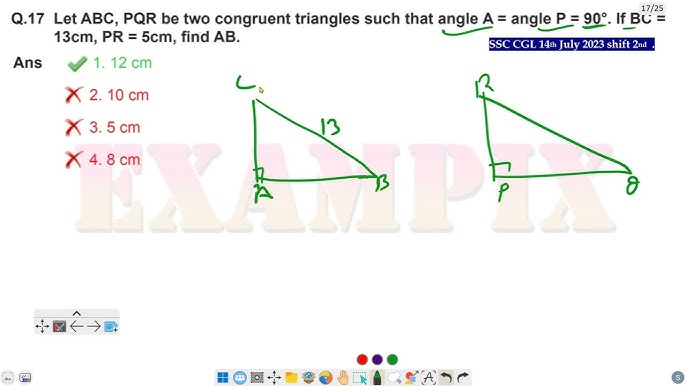
When it comes to geometry, proving that two triangles are similar is a fundamental concept. The notation Which would prove that δabc ~ δxyz? select two options. indicates that triangles ABC and XYZ are similar, meaning that their corresponding angles are congruent and their corresponding sides are proportional. But how do you prove that ΔABC is similar to ΔXYZ? In this comprehensive article, we will delve into the concept of triangle similarity, explore the criteria used to prove that Which would prove that δabc ~ δxyz? select two options., and provide clear steps and options for selecting the best methods to prove this similarity.
What is Triangle Similarity?
Before discussing how to prove that Which would prove that δabc ~ δxyz? select two options., it’s essential to understand what it means for two triangles to be similar. Two triangles are considered similar if:
- Corresponding Angles are Congruent: Each angle in one triangle is equal to the corresponding angle in the other triangle.
- Corresponding Sides are Proportional: The lengths of the corresponding sides of the two triangles are in the same ratio.
In mathematical terms, if triangles Which would prove that δabc ~ δxyz? select two options. are similar, the following conditions hold:
- ∠A = ∠X, ∠B = ∠Y, and ∠C = ∠Z (corresponding angles are equal)
- AB/XY = BC/YZ = CA/ZX (corresponding sides are proportional)
These two conditions lead us to a few important theorems and postulates that can be used to prove triangle similarity. The key methods include the AA (Angle-Angle) Criterion, SSS (Side-Side-Side) Criterion, and SAS (Side-Angle-Side) Criterion.
Criteria to Prove Triangle Similarity
There are three primary methods to prove that two triangles are similar:
- AA (Angle-Angle) Similarity Criterion: If two angles of one triangle are congruent to two angles of another triangle, then the triangles are similar.
- SSS (Side-Side-Side) Similarity Criterion: If the corresponding sides of two triangles are proportional, then the triangles are similar.
- SAS (Side-Angle-Side) Similarity Criterion: If one angle of a triangle is congruent to one angle of another triangle, and the lengths of the sides including these angles are proportional, then the triangles are similar.
Now, let’s explore each of these methods in detail and determine which two options you can select to prove that Which would prove that δabc ~ δxyz? select two options..
Option 1: Proving Similarity Using the AA (Angle-Angle) Criterion
What is the AA Criterion?
The Angle-Angle (AA) Criterion states that if two angles of one triangle are congruent to two angles of another triangle, the triangles are similar. This is based on the fact that if two angles are congruent, the third angle must also be congruent, as the sum of angles Which would prove that δabc ~ δxyz? select two options. in a triangle is always 180°.
Step-by-Step Proof Using AA Criterion
- Identify the Corresponding Angles: First, identify which angles in ΔABC correspond to which angles Which would prove that δabc ~ δxyz? select two options. in ΔXYZ. For example:
- ∠A corresponds to ∠X
- ∠B corresponds to ∠Y
- ∠C corresponds to ∠Z
- Prove the Angles are Congruent: To use the AA criterion, you need to show that at least two pairs of corresponding angles are congruent:
- If ∠A = ∠X and ∠B = ∠Y, then the two triangles will automatically be similar.
- The third pair of angles, ∠C and ∠Z, will also be congruent because the sum of the angles in both triangles must be 180°.
- Conclude the Triangles are Similar: Once you’ve proven that two pairs of angles are congruent, you can conclude that Which would prove that δabc ~ δxyz? select two options. based on the AA criterion.
Why Choose the AA Criterion?
The AA criterion is often the easiest and quickest method to prove triangle similarity because it only requires you to compare angles. This criterion is especially useful when working with problems where angle measures are given or can be easily determined.
Option 2: Proving Similarity Using the SSS (Side-Side-Side) Criterion
What is the SSS Criterion?
The Side-Side-Side (SSS) Criterion states that if the corresponding sides of two triangles are proportional, then the triangles are similar. This criterion relies on the idea that if all sides are proportional, the angles must also be congruent.
Step-by-Step Proof Using SSS Criterion
- Identify the Corresponding Sides: Identify which sides of ΔABC correspond to which sides of ΔXYZ. For example:
- AB corresponds to XY
- BC corresponds to YZ
- CA corresponds to ZX
- Prove the Sides are Proportional: To use the SSS criterion, you need to show that the ratios of the corresponding sides are equal. Specifically, you must demonstrate that:
- AB/XY = BC/YZ = CA/ZX
- Conclude the Triangles are Similar: Once you’ve proven that the ratios of the corresponding sides are equal, you can conclude that Which would prove that δabc ~ δxyz? select two options. based on the SSS criterion.
Why Choose the SSS Criterion?
The SSS criterion is ideal when the side lengths of the triangles are given or can be easily calculated. It’s also useful in problems where you don’t have access to the angles but can measure or compute the sides.
Option 3: Proving Similarity Using the SAS (Side-Angle-Side) Criterion
What is the SAS Criterion?
The Side-Angle-Side (SAS) Criterion states that if one angle Which would prove that δabc ~ δxyz? select two options. of a triangle is congruent to one angle of another triangle and the sides including these angles are proportional, then the triangles are similar.
Step-by-Step Proof Using SAS Criterion
- Identify the Corresponding Sides and Angles: Identify which angle in ΔABC corresponds to which angle in ΔXYZ, and which sides are adjacent to that angle. For example:
- ∠A corresponds to ∠X
- AB corresponds to XY, and AC corresponds to XZ
- Prove the Angle is Congruent and the Sides are Proportional: To use the SAS criterion, you need to show:
- ∠A = ∠X
- AB/XY = AC/XZ (the sides adjacent to the angle must be proportional)
- Conclude the Triangles are Similar: Once you’ve proven that one pair of angles is congruent and the adjacent sides are proportional, you can conclude that Which would prove that δabc ~ δxyz? select two options. based on the SAS criterion.
Why Choose the SAS Criterion?
The SAS criterion is a good option when you have information about an angle and the two sides adjacent to that angle. It is particularly useful when you don’t have all the side lengths or all the angle measures but have enough information to apply this method.
How to Select the Best Option for Proving Which would prove that δabc ~ δxyz? select two options.
When deciding which method to use, consider the following:
- AA Criterion: This is the simplest option if you can easily identify and prove that two pairs of corresponding angles are congruent. It doesn’t require any side length information.
- SSS Criterion: This is the best option if you know the lengths of all corresponding sides and can prove that they are proportional. No angle information is needed.
- SAS Criterion: This method is ideal if you know one pair of corresponding angles and the lengths of the sides adjacent to that angle.
In most cases, the AA criterion is the easiest to apply, but the SSS and SAS criteria are just as valid and may be more appropriate depending on the given information.
FAQs
1. What does it mean for two triangles to be similar?
Two triangles are similar if their corresponding angles are congruent, and their corresponding sides are proportional. This means the triangles have the same shape but not necessarily the same size.
2. Can two triangles be similar if they have the same area?
No, the area alone does not determine similarity. Triangles with the same area can have different shapes. To prove similarity, you need to show that the corresponding angles are congruent and the sides are proportional.
3. Is there a difference between congruent and similar triangles?
Yes, congruent triangles are identical in shape and size, meaning all corresponding sides and angles are equal. Similar triangles have the same shape but may differ in size, meaning the corresponding angles are equal, but the corresponding sides are proportional rather than equal.
4. What is the easiest way to prove that two triangles are similar?
The easiest way to prove similarity is typically the AA (Angle-Angle) criterion. If you can show that two pairs of corresponding angles are congruent, the triangles are similar.
5. Can two triangles be similar if only one pair of angles is congruent?
No, one pair of congruent angles is not sufficient to prove similarity. You need at least two pairs of congruent angles (for AA criterion) or proportional sides (for SSS or SAS criteria).
Conclusion
Proving that Which would prove that δabc ~ δxyz? select two options. involves selecting the appropriate method based on the available information. The AA, SSS, and SAS criteria all provide valid ways to prove triangle similarity, each with its advantages depending on whether you have information about angles, sides, or both. By understanding and applying these methods correctly, you can confidently demonstrate that Which would prove that δabc ~ δxyz? select two options.